Functions and Graphs
Review of some topics from Algebra
- Sketch the set of points described by
|2x-3|<1
- Describe the set of points –2<x<7 using
absolute values
- What is the equation for the circle of radius 3
centered at (1,-2)?
- Give the equations of the following lines in
point-slope form.
a.
the line through (2,3)
with slope –1
b.
the line through (-2,5)
and (1,3)
c.
the line parallel to
y=2x+6 through (1,1)
d.
the line through the
origin perpendicular to the line y – 2x = 5
- Sketch the set of points described by x^2
+(y+3)^2 = 4
Review of some
topics from Trigonometry
- Show on the unit circle which angles have
- sines of .4 .
- cosines of -.3
- tangents of 3
Functions
- Which of the following define y as a function of
x? Why?
- y = x^2 + x
- x^2 + y^2 = 1
- y = 3
- sin(y) = x
- Let f(x) = sin(x) and g(x) = x^2. What is
f(g(x))? What is g(f(x))? Are they the same? Plot them. (Use MAPLE and
choose a reasonable x range.)
- Which of the following are polynomials?
- x^3 – x + 13
- (x+1)^(1/2)
- (x-3)^2
- (x+1)/(x-2)
- Plot the functions in exercise (9).
- Tell me how long this assignment took. What was
hardest?
Inverse Functions, Logarithms &
Exponentials
Inverse functions
- Plot the following. (Use MAPLE.) Which have
inverses? Why? Find them.
- x^3
- x^2 + x + 1
- (x+1)/(x-2)
- x – 1/x
Graphs of trig functions
- Plot all six trig functions. What are the
periods?
- Plot 2*sin(3*x) – cos(3*x). What is the period?
What is the amplitude?
Inverse trig
functions
- Evaluate the following:
- sin(arccos(.3))
- cos(arctan(10))
- tan(arcsin(-.2))
- What is sin(arcsin(x))? How about
arcsin(sin(x))? Explain.
- Let A = the angle in the second quadrant with
sine = .7, and find all five other trig functions of A.
Exponentials
- LEARN the rules of exponents!
- Graph 3^x, 3^(-x), (1/3)^(x). What do you
notice? Prove it!
Logarithms
- Assume that x = b^y. What does this say about
the log base b of x? Now take the log base a of both sides of x = b^y.
Derive the change of base formula.
- Plot log base 10 of x, log base 2 of x, and the
natural log of x.
Story problems!
- How much interest does $1000 earn at 5% per year
if it is compounded
- monthly?
- daily?
- hourly?
- If T(t) is the temperature of an object, and
Troom is the room temperature, then T(t) is given by an equation of the
form T(t) = Troom + [T(0) – Troom]*exp(-k*t). (T(0) is the temperature at
time 0, and k is a constant.) Suppose my coffee starts out at 180 degrees
Fahrenheit, and after 5 minutes it is 140 degrees. Assuming room
temperature is 70:
- Find k
- Find the temperature after 15 minutes.
- When will the temperature be 100?
- Tell me how long this assignment took. What was
hardest?
Derivatives – slopes, tangents,
"zooming"
- Take
the function f(x) = x^2, and a point on its graph, (a,a^2) (Choose your
favorite a.) Draw the lines through the points at x = a and x = a +h for h
= 1, .5, .1 and then sketch the tangent line.
- Do
the same thing with some negative h values, getting close to 0.
- Now
try the lines from x = a-h to x = a+h.
- Have
MAPLE simplify the expression [f(a+h) – f(a)]/h. What happens as h gets
small? How does this relate to what you did above?
- Now
define f as a function in MAPLE, and take its derivative (using either the
D or diff operators.)
- What
is the equation of the tangent line?
- Repeat
exercises 1 – 6 with a couple of other functions.
- Plot
a polynomial in MAPLE and choose a point on the graph. By choosing the
horizontal and vertical ranges in the plot function, "zoom" in
symmetrically about your point. What do you observe?
- Use
diff or D to find the derivative of your polynomial. What is the tangent
line at your point? Plot the polynomial and the tangent line on the same
graph and repeat exercise 8.
- Repeat
exercises 8 – 9 for another function. Use a trig function this time.
- Plot
the following functions and determine just from the graph where the
derivative is positive and where it is negative
- x^3 + 2*x^2 – x – 2
- sin(x)
- x*exp(-x)
- ln(x)
- And our usual last question, how long did this take and what was
the hardest?
Rates of Change
- The position of an object is described by s(t) =
(t^2+2*t)/(t^2+t+1). Plot this function. Also, find and plot the velocity
and the acceleration of the object. Discuss.
- Starting from ground level, a ball is thrown up at 5 m/s. When
does it hit the ground? What was its average velocity? Average speed?
- How fast does a ball hit the ground if it is thrown upward at 6
m/s from the top of a 10 m building? What if it were thrown down at
6 m/s?
- What is the volume of a sphere in terms of the radius? What is the
rate of change dV/dr? Does this look at all familiar? Explain
- Repeat the previous exercise (which I believe to be number 4) with
a cube.
- How fast should a ball be thrown upward to just barely hit the ten
foot ceiling?
- The thickness of the layer of lime in your water pipes grows at a
constant rate. If your pipes have inside diameter .75 inch, how fast is
the open cross section changing, relative to the thickness of the lime
layer, when the layer is .1 inch?
- Use the tangent line to the curve y = x^(1/2) at some appropriate
point, to approximate the square root of 3. Now use a closer point, and
improve your approximation.
- Plot the curve and the first 2 tangent lines to approximate the
root of x^3 – 2*x^2 – 2*x – 2
- When you measure the diameter of a circle, you find it to be 6 cm,
to within 1%. How accurately can you calculate the area?
- Suppose a soccer ball is made of leather 1/8 inch thick. If the
outside diameter is 9 inches, and the density of leather is assumed to be
.64 oz/cubic inch, how much does the ball weigh?
- How long did this take and what was the hardest?
Chain Rule
- Let
f(x) be the square root of x, and g(x) be 1/(x^2+1). What are the range
and domain of f(g(x))? Of g(f(x))?
- What
are the derivatives of f & g? From the chain rule, what should the
derivatives of the functions f(g(x)) and g(f(x)) be? Check this.
- A
boy is flying a kite. If the kite is moving 10 ft/sec horizontally south,
and is 60 feet above the ground, how fast is the string unwinding when the
kite is 100 feet south of the boy?
- A
1.6 meter tall woman is walking past a 3 meter lamppost. If she is walking
at 2 m/s directly away from the lamp, how fast is the length of her shadow
changing when she is 5 m away?
- A
lighthouse is 1 mile offshore, due west. You are on the shore, 2 miles
north of the point opposite the lighthouse. If you see the flash every 15
seconds, how fast is the beam of light moving when it passes you?
- A
trough is triangular in cross section, an isosceles triangle with sides 12
inches, and top 10 inches. The trough is 40 inches long. How fast is the
depth changing if you are pumping one cubic foot per minute into the
trough?
- In
a moment of foolishness, you tie your dog to the foot of the 4 meter ladder
you are climbing. When you are 1.5 m from the top, the dog leaves, at ¾
km/hr, chasing a rabbit. How fast do you hit the ground?
- A
light is attached to a 13 inch radius bicycle tire, at a point 8 inches
from the center. If Harvey rides the bicycle at 15 mph, how fast does the
light move up and down at its fastest?
- And,
as usual, how long and which was hardest?
Implicit
Differentiation
Parameterized
functions
- Consider the circle x^2 + y^2 =1. Find the slope of a tangent to
the circle two ways: a) by solving for y, and taking the derivative and b)
by implicit differentiation.
- Repeat the previous problem with x = y^2.
- Find the derivative of exp(-x), exp(a*x), exp(f(x)).
- Use implicit differentiation to find the derivative of arccos(x).
- Use implicit differentiation to find the derivative of arctan(x).
- Use implicit differentiation to find the derivative of ln(x).
- Find the derivative of x^(1/x)
- Find a parametric equation for the ellipse (x^2) + (y^2)/4 = 1.
Find the derivative three ways: a) solve for y, b) implicitly, and c)
using the parametric form.
- Suppose a reflector is attached 8 inches from the center of a
24-inch diameter bike wheel. If the bike wheel rolls with out slipping,
find parametric equations for the position of the reflector. Plot it.
- Try putting the reflector at different distances from the center
and plot.
- And, as usual, how long and which was hardest?
Max – Min Problems
- Find
the critical points of x^3-2x^2+x-2 on the interval [0,5]. Identify the
type of each. Plot.
- Find
the local and global minima and maxima of x^(2/3) on the interval [-1,2].
Plot.
- If
two numbers add to 12, what is the biggest their product can be?
- A
poster is to have 150 square inches of printed material. If we want a 2 inch
margin at the top, and 1 inch margins on the other three edges, what
dimensions use the smallest amount of paper?
- The
material for the top of a cylindrical can cost three times as much as the
material for the sides and bottom. What dimensions should the can have to
hold a fixed amount?
- An
off shore oil rig is 3 km west of the shore. We wish to pump the oil to a
location on the shore 5 km north of the rig. If it costs 1.8 times as much
per kilometer to build an underwater pipeline as one on land, how should
we design our pipeline?
- To
make pompoms in our school colors, we will have expenses of $100 to rent
the Acme PomPomPlant, and then $.25 / pompom in materials. We believe that
we can sell 500 pompoms if we charge $1, and that if we charge $1.50 we
will only sell 300. Assume that the number sold is a linear function of
cost. How much should you charge to make the biggest profit?
- Strength
of a rectangular beam is proportional to width times (depth)^2. What are
the dimensions of the strongest beam that can be cut out of a 12 inch
diameter log?
- A
line in the first quadrant is tangent to the graph of y = 1/x^2. How can
we minimize the area between the line and the axes?
Max – Min Problems
- Imagine
a function with positive second derivative. Start at x=0 with slope –2,
and approximate the function with a piece of straight line. Suppose that
the slope increases by one every time x increases by one, and continue
approximating by pieces of straight line (do this by hand, not MAPLE).
What does your sketch look like?
- Must
a function with positive second derivative go up?
- Consider
the function x^(4/3), on the interval [-2,2]. Find the critical point.
What does the second derivative test say? Plot the function and explain.
- If
the speed of light in water is about ¾ the speed of light in air, how much
does a beam of light striking water at an angle of p /8 bend?
- A
pyramid consists of 4 equilateral triangles around a square base. If this
is to be cut and folded out of a single square piece of paper (base in the
center, tops of triangles in the corners), maximize the volume.
- What
is the longest pipe that can be carried horizontally around a corner from
a 5 foot wide corridor into an eight foot wide one?
- We
are told that if 60 grapevines are planted per acre, each vine will
produce 120 lbs. of grapes, but that each additional vine per acre reduces
the average yield per vine by 3 lbs. How many vines should be planted to
maximize the yield per acre?
- The
labor to tend the grape vines costs $4 per vine per season. The grapes
sell for 65 cents per pound. How many vines should be planted to maximize
the profit?
- Taxes
on the land are $50 per acre. Does this change the best strategy? How?
- How
would you build the cost of the vines into your model?
- Approximate the area under the curve y = x^2 + x between x=1 and
x=3 using 10 rectangles and (a) the left endpoint (b) the right endpoint,
(c) the midpoint.
- Repeat problem 1 with the upper half of the circle x^2 + y^2 = 1.
Compare to the exact answer.
- Prove that
![]()
- The trapezoid formula approximates an area by using a straight
line on each subinterval; this give tall, skinny trapezoids. Write out a
general formula for the trapezoid formula to approximate the area under
f(x) from x=a, to x=b. Now for n=5 expand out the sum. What do you see?
- Standard last question J
- Show that the fundamental theorem is true for f(x) a straight line
(get the area geometrically).
- Find an antiderivative for (a) x^3 + 2*x^2 – x +1 (b) sqrt(x) (c)
cos(x) (d) sin(x)
- If diff(f(x),x) = diff(g(x),x) –1, what can you say about f and g?
- What is the antiderivative of x^n? For what values of n is this a
problem?
- Consider
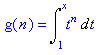
Sketch a graph that
represents this integral. Does this graph make sense at n = -1? Evaluate the
integral, and choose a value for x. Plug in values of n getting closer and
closer to –1. Do you approach a limit?
- Evaluate the integral in problem 5, for n = -1, using MAPLE. Does
this agree with the limit you got at the x value you chose?
- Evaluate the integral of sin(x) from 0 to 2p using MAPLE. Does this make sense as an area?
Sketch the graph. What do you see? Now find the actual area between sin(x)
and the axis between x = 0 and x = 2p .
- Let H(x) = 0 for x<0 and 1 for x>0. Sketch H. What is the
integral from 0 to x of H? Sketch it. How about the integral from –1 to x
of H? From 2 to x?
- Now let G(x) be 0, for x<0; x, for 0<x<2; and 2, for
x>2. Repeat the previous problem for G.
- Standard last question.
- Set
up the volume of a cone as an integral. Evaluate.
- Set
up an integral to find the volume of an equilateral tetrahedron. Evaluate.
- Consider
the solid obtained by rotating the region in the first quadrant between
x=0, y=0 and y = 2 – x^2 around the x – axis. Set up the integrals for the
method of shells, and the discs. Evaluate both.
- The
wetted face of a dam is a trapezoid 40 feet wide at the top, and 30 feet
wide at the bottom, at a depth of 12 feet. The face is slanted do that the
bottom is five feet in from the top. Find the total hydrostatic pressure
on the face.
- A
water tank is a sphere, 3 m in diameter, 15 m above ground level. How much
work does it take to fill the tank half way? All the way?
- Find
the total work to put a one ton satellite in geo-synchronous orbit,
approximately 24,000 miles up. (You may assume the earth is a sphere with
radius 4000 miles. Force due to gravity is proportional to 1/distance^2,
and you know what it is at distance = 4000 miles.)
- Set up integrals to find the arc length of y = x^3 from (1,1) to (3,27) by integrating with respect to (a) x and (b) y. Evaluate them both.
- Set up three different integrals to find the circumference of a circle, integrating with respect to x,y and a parameter q . Which looks easiest?
- Find the surface area of a sphere using a surface area integral.
- Do the same for a cone.
- Find the circumference of the ellipse x^2/a^2 + y^2/b^2 = 1. Use a parametric equation.
- Find the surface area, and the volume, of the solid obtained by rotating the area bounded by y = (1-x^2)/3 and the x-axis about the x-axis.
- Standard last question.
- Find the centroid of the region bounded by 1 – x^2 and the x – axis.
- Use the theorem of Pappus to find the centroid of a semicircle with out integrating.
- Set up and evaluate the integrals to check your answer in #2.
- Let g(x) = 1/f(x) and apply the product rule to f(x)*g(x). Solve for dg/dx.
- Use the result in the previous problem, and the product rule to get a formula for the derivative of u(x)/v(x).
- Use integration by parts to integrate x*exp(-2*x)
- Use integration by parts to integrate x^2*sin(3*x)
- Use integration by parts to find the area under x*ln(x) between 1 and 5.
- Use the substitution x = sin(t) to integrate 1/sqrt(1-x^2)
- Find the substitution to make 1/(x^2+x+1) = 1/(u^2+1). Integrate (using Maple) both ways.
- What are the three most important things to change the next time we offer this class?