ST 552

Calculus on a Computer

Assignment 10 – Anti-derivatives & the Fundamental Theorem of Calculus

1. Geometrically, get a formula for the area under the line y=mx+b between x=a and x=c. Show that this matches what you get from the fundamental theorem of Calculus.

2. Use MAPLE to find anti-derivatives of the following. Plot them. What does it mean when the anti-derivative is decreasing?

a.

b.

c.

3. Evaluate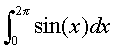. Does this make sense as an area? Sketch the graph. What do you observe? Now find the actual area bounded by the curve and the x axis.

4. What is the anti-derivative of ? For which value of n is this a problem?

5. Consider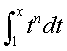. Sketch a picture that represents this integral. Does your picture make sense for n=-1? Evaluate the integral for general n, and choose a value for x. Substitute various values of n approaching -1. Do you approach a limit?

6. Now use Maple to evaluate the integral in exercise 5 at n=-1. Substitute in the value of x you chose. Does this agree with the limit you got in exercise 5?

7. If 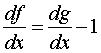, what can you say about f and g?

8. Let . What is the integral of H(x)

a. From 0 to t?

b. From -1 to t?

c. From 2 to t?

(Don’t forget negative t values.)